Graph - Degree, Indegree and Outdegree
Next - Graph Adjacency Matrix >>
In this page, we will learn about quantifying the size or complexity of a graph.
Quantifying the Graph
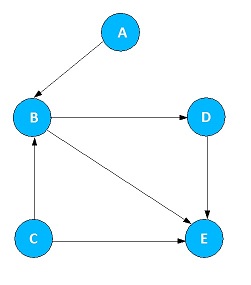
Degree of a Vertex
Degree of vertex is the number of lines associated with a vertex. For example, let us consider the above graph. Degree of a vertex A is 1. Degree of a vertex B is 4. Degree of a vertex C is 2.
Indegree of a Vertex
It is the number of arcs entering the vertex. For example, let us consider the above graph. Indegree of vertex B is 1.
Outdegree of Vertex
It is the number of arcs leaving the vertex. For example, let us consider the above graph. Outdegree of vertex B is 3.
<< Previous - Graph Properties
Next - Graph Adjacency Matrix >>









