Data Structures - Tree Traversal
- Tree traversal is the action of visiting all the nodes in the tree exactly once.
- There are three ways to traverse a tree.
- Inorder Traversal
- Preorder Traversal
- Post Order Traversal
- Primary purpose of tree traversal is to search and locate an item in the tree
Traversal process
First step is to define a traversal process depending on the type of traversal. Then, repeatedly call the traversal process for each node.
Traversal process is coded in a procedure in RDBMS constructs, or using functions in languages like C or C++, or method in languages like Java. Basic process and idea remains the same.
In Order Traversal
In In-order traversal process or function, the nodes on the left are traversed first, then the root node and then the nodes on the right.
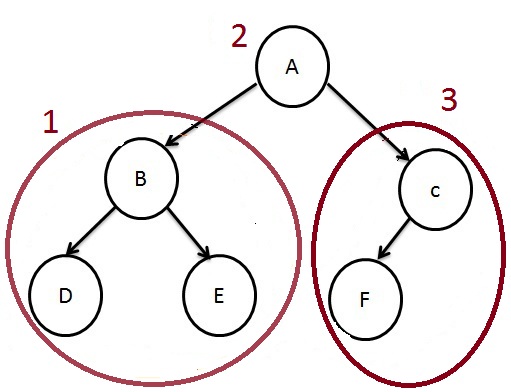
Based on the process, we traverse the left subtree recursively by calling In Order function, then process the root node, and then traverse the right subtree recursively by calling In-Order function.
The output of the above tree is.
D-->B-->E-->A-->F-->C Pre-Order Traversal
In Pre-Order traversal, the root node is visited first, then the left subtree and right subtree are traversed.
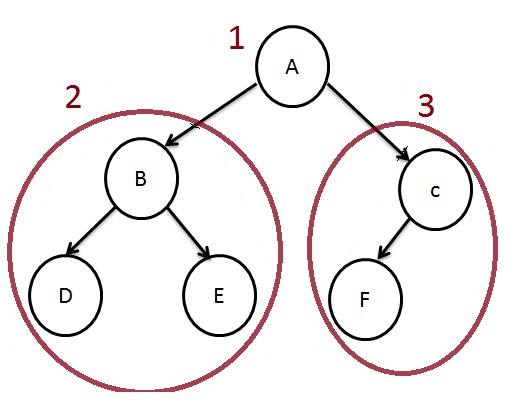
Based on the process, we first process the root, then traverse the left subtree recursively by calling Pre-Order function, and traverse the right subtree recursively by calling Pre-Order function.
The output of the above tree is
A-->B-->D-->E-->C-->F Post-Order Traversal
In Post-Order traversal, we will first traverse the left nodes, then the right nodes and then traverse the root node.
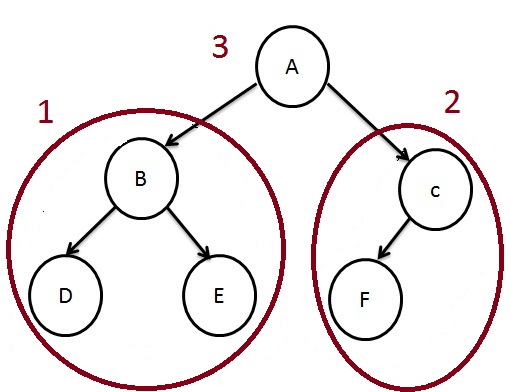
Based on the process, we traverse the left subtree recursively by calling Post-Order function, then traverse the right subtree recursively by calling Post-Order function and finally process the root node.
The output of the above tree is.
D-->E-->B-->F-->C-->A 







